�D�� A
�˽c�l
��J��: pack.in /��X��: pack.out
�ٰO�o�C�Ӽڤڮ�X��^�Ӥ�W�j�]�p�]�����~���e�����H���F�n��ˤU�̦h���F��A�o�̥X��ɥ��w�a�ۤ�A�i�H�Q���o���h���c�l�C
���M�A���ۤj�p�Žc�l�X��O�۷��ª��@��Ʊ��C�o�����ڤڮ᳣���o��p�c�l�κɤ@����k�A���j�c�l�̭��C�ӧA���u�@�A�N�O�P�_��ӽc�l�ण��˦b�@�_�C
���F��K�_���A�ڭ̶ȦҼ{�x�Ϊ��c�l�A�åB�u�Ҽ{���e�A�c�l�S���p�סA�ӿ�X�u�ݧP�_�j�x�Υi�_��o�U�p�x�ΡC
�`�N�G�b���D�ءA�p�c�l�b�j�c�l�̭����O�K�����A���Ҽ{�ש��p�C
n
��J�ɻ���
��J�C�榳�|�Ӥp��30000���Ʀr�A�Τ@�Ӫť�����j�A�e��ӼƦr���O�N���Ĥ@�ӯx�Ϊ����B�e�A���ӼƦr���O�N���ĤG�ӯx�Ϊ����B�e�C��J�̫�@�欰�@�ӼƦr0�C
n
��X�ɻ���
��C�@�մ��ո�ƿ�X�@��G�p�G�䤤�Y�ӯx�Υi�H������J�t�@�ӯx�Ρ]�i�H�K����^�h��Xyes�A�_�h��Xno�C
n
�d�ҿ�J
2345 6789 12345 16789
1 100 50 2
0
n
�d�ҿ�X
�D�� B
�j�ƭ��k
��J��: big.in / ��X��: big.out
�g�@�{���p���ӥ���Ƭۭ������G�C
��J��ӥ���ơA�C�ӥ���Ƴ̦h��Ƭ�500��ơA�p��X��ۭ����ȫ��X�C��J����ƨC�@�榳��ӥ���ơA�H�@�ӪŮ��}�A�{��������s��Ū�J��ơA����J��
0 ����A�M��̧ǿ�X�C�@�檺�p��G�C
n
��J�ɻ���
�C���ӥ���ơA�H�Ů�j�}�A�̫�@��H0�����A�C�@�r����Ҥp��500�Ӧr���C
n
��X�ɻ���
�C���X�p���Ƭۭ������G�C
n
�d�ҿ�J
1 2
1020304050 6070809000
10203040506070809000 777777777777
0
n
�d�ҿ�X
2
6194071009476450000
7935698171380471301828611593000
�D�� C
���쪺�q�Ʀr�C��
��J��: guess.in /��X��: guess.out
���@�زq�Ʀr���C���A�Ѥ�������U�q�U�@�ӥ|��ƪ����K���X�A�o�Ӹ��X������зǬO�C�Ӧ�ƪ��Ʀr���������ܢ������B���ۦP���Ʀr�A���ɶ}�l�Ѥ@��q��踹�X�A���h�̾کҲq�����X�P�ۤv�����K���X���A�^���Ҳq���X�����T�ʡA�Ӧ^�����W�h�p�U�G
���p�Ҳq���X�P���K���X�������ơ]�ӤQ�ʤd��^�ۦP�A�h�H�ϨӪ��ܡC���p�Ҳq���X�P���K���X���Ʀr�ۦP�A���Ҧb��m���P�A�h�H�ШӪ��ܡC�Ҧp�G���K���X�����������A�h�G
�q���������A�h�^�����Ϣ��СC
�q���������A�h�^�����Ϣ��СC
�q���������A�h�^�����Ϣ��СC
�p���Ѥ���������y�V���o�ݡA�øg�ѩұo�쪺�^���Ӥ��R�k�ǥH�q�X��誺���K���X�A�H���q��̬��u�ӡC
�{�b�A���P�B�Ͷi��o�Ӻ�i�������q�Ʀr�C���A���ɥH�i���̫ᶥ�q�A�A�w�g�q����⯵�K���X�������Ʀr�]���������^�A�u�O�o�ǼƦr��m����A�ЧA�g�@�ӵ{���Ӥ��R���ҵ����Ҧ���ơA�ӸѥX�Ҧ��i����T���סI
n
��J�ɻ���
��J�ɤ����@�թΤ@�եH�W����ơC�C�@�ժ���ƬO����* ���ܸ�ƶ}�l�A�H**���ܥ��ո�Ƶ����A�̫�åH***�����ɮ���
�A�C�@���ƫe�|�X���A�q�����X�A�۬���誺�^���A�Ҧ���������ƬҬ��q���|�X�����ΡA�C�@����ƬҬ����۹�^������ơC�]�Ҧ��^��r�������j�g�^�C
n
��X�ɻ���
�бN�C�դ��ɸ�ƥi����T����(�ܤ֦��@��)�Ѥp�ܤj���ǦC�X�A�C�@�ӵ��פ@�C�A�åH* ���C�յ��ת��}�l�H��**���C�յ��ת������A�̫�H*** ������ɮ�X�������C
n
�d�ҿ�J
*
47652A2B
67450A4B
**
*
47561A3B
76540A4B
**
***
n
�d�ҿ�X
*
4567
**
*
4765
5476
6745
**
***
�D�� D
�O�i�����ƪ����j�i�}
��J��: fib.in / ��X��: fib.out
�O�i�����ƬO�@�ؼƾǯżơA�ڭ̩w�q���żơG
�e�Q�ӶO�i������f(0)~f(9)
���O�O1, 1, 2, 3, 5, 8, 13, 21, 34, 55�C
�ӶO�i�����ƪ��p��`�`�O���j�t�⤤����¦���νm���D�A�H�U�O�@�q²�檺�O�i�����ƻ��j�禡(��c�y���Ӫ���)�C
int fibonacci(int n) {
if(n<=1) return 1;
else return fibonacci(n-2)+fibonacci(n-1);
}
�ڭ̨ӬݬݩI�s
fibonacci(4)�����j�i�}(�H�U²��f(4))�����ΡA�Ӥ��R���j�p��O�i�����Ʃһݭn�I�s��ƪ����ơC
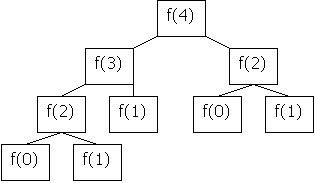
�ѤW�ϥi�H�o�{�A�ѩj�i�}�`�`�n�p��w�p��L���O�i�����ơA�]���ݭn�I�s��ƪ����Ʒ|�������ܧ֡C�W�Ϥ��i��f(4)�@�@�I�s�F9����ơA�Ө�L�Ҧp�G
f(0), f(1), f(2), f(3) ���O�I�s�F1, 1,
3, 5����ơC
�o���D�ةҭn�ݪ��N�O�A���w1�Ʀrn�A��X�Q�λ��j�i�}��fibonacci(n) �һݻ��j�I�s��ƪ����ơC
n
��J�ɻ���
���ո�ƪ��}�Y��1�ӼƦrn�A���U�Ӥ@�@��n��A�C1��1�ӼƦr(a1, a2, a3,�K, an)�A (0 £ a1, a2,
a3,�K., an £ 45) ���ܱ��p�⪺�O�i�����ơC
n
��X�ɻ���
���C1�ӼƦr�A��X���j�i�}�ӼơA�һݻ��j�I�s��ƪ����ơC
n
�d�ҿ�J
n
�d�ҿ�X
�D�� E
�ߥ��Y
��J��: rock.in / ��X��: rock.out
���@�ӴI�ηQ���k���Ӧn�k�J�A�L�Q�X�F�@�Ӥ�k�A����������B�������b�@�_���ɡA�C�ӤH���t��@�ƥ��Y�A�Ч��B�̱q�ۤv���@�Ƥ��ɶq�ߥX�̤j���@���C�ܦh�H�@�����߾ߡA���ɦ^���U�ߡA�u���@��C�~�A�j�����ݤ��@���j���Y��K�@��������I�C�I�λ{���L����ñ��Ҧ��A�b���F�k�ध�ᥲ�w����M�@�A�Ӥ��|����L�H�@����߾ߡA��ۤv�ұo�@���L�k���N�A�K��F�L���F�ɧִB�C
�o�^�I�ΤS�n���k��F�A�@�i�ߥ��Y���ɪ����i�S�K�b���f�C�����̦��F�W���g��A���N�������x�A�dzƾߤ@���j���Y�N������I�C���@����ɷ|���~�o�{�W�h���w�ܧ�p�U�G
1.
�C�ӤH�٬O�u��ߦۤv���@�ƪ����Y�C
2.
�u��e�i�����h�C
3.
�i�H�ߤ��u�@�����Y�A����Ӿߪ������e�w�g�߰_�����n�j�~��C
4.
�ɶq�̦߳h�����Y�C
�����@�Ӭ��I�μg�{�������u�A�A�M�w�n�n�n�@�i���~�A���A���H�ݫ�C�ѩ����ӻO�A�A�w�g�����a���D�C�����Y���j�p���Y�A�{�b�A���ؼЬO�g�X�@�ӵ{����ߨ�̦h�����Y�C
n
��J�ɻ���
��J�|�Ѥ@�Ӿ��N�}�l�A���ܴ��ո�ƪ����ơC�C�@�����ո�Ʒ|�Ѥ@�Ӿ��m�}�l�A���ܥ��Y���ƥءA���U�ӬOm��A�C�@�榳�@�Ӿ��(���i�ର�t�ơA�A���{���n��B�z)�A���ܥ��Y���j�p���Y�A�Ʀr�V�j���Y�]�V�j�C(1<=m<=100000)�C
n
��X�ɻ���
�C�@�����ո�ƦL�X�@�ӼƦr�A���̦ܳh�i�H�������Y�ơC
n
�d�ҿ�J
2
5
1
2
3
4
5
5
5
4
3
2
1
n
�d�ҿ�X
![]()
